用等角共轭解决2014年韩国数学奥林匹克P2几何
证明
作\(W'\)为\(W\)关于\(CF\)的对称点.因为\[AE\cdot AL=\frac12AL\cdot AC=\frac12 AB^2=AB\cdot AF,\]所以\((ELFB)\).
充分性
若\(AW=PW\),则\(W\)为\(\triangle ACP\)外心.熟知\(W,H\)关于\(\triangle ACP\)等角共轭.因为\[\angle W'CB=\angle WCA=\angle FCP,\] \[\angle W'BC=\angle WAC=\angle HAF=\angle HBJ,\]所以\(W',J\)关于\(\triangle BCF\)等角共轭.所以\(\angle WFC=\angle W'FC=\angle MFB\Rightarrow \angle LFM=90^\circ\Rightarrow (LEFM)\Rightarrow (BEFM)\).
必要性
若\((BEFM)\),\(\angle LFM=90^\circ\).去\(J\)关于\(\triangle BCF\)的等角共轭点\(W'_1\).显然\(W',W'_1\)在\(BC\)中垂线和\(FJ\)等角线上,于是\(W'_1=W'\).所以\(W\)为\(\triangle ACP\)外心,\(AW=PW\) \(\square\)
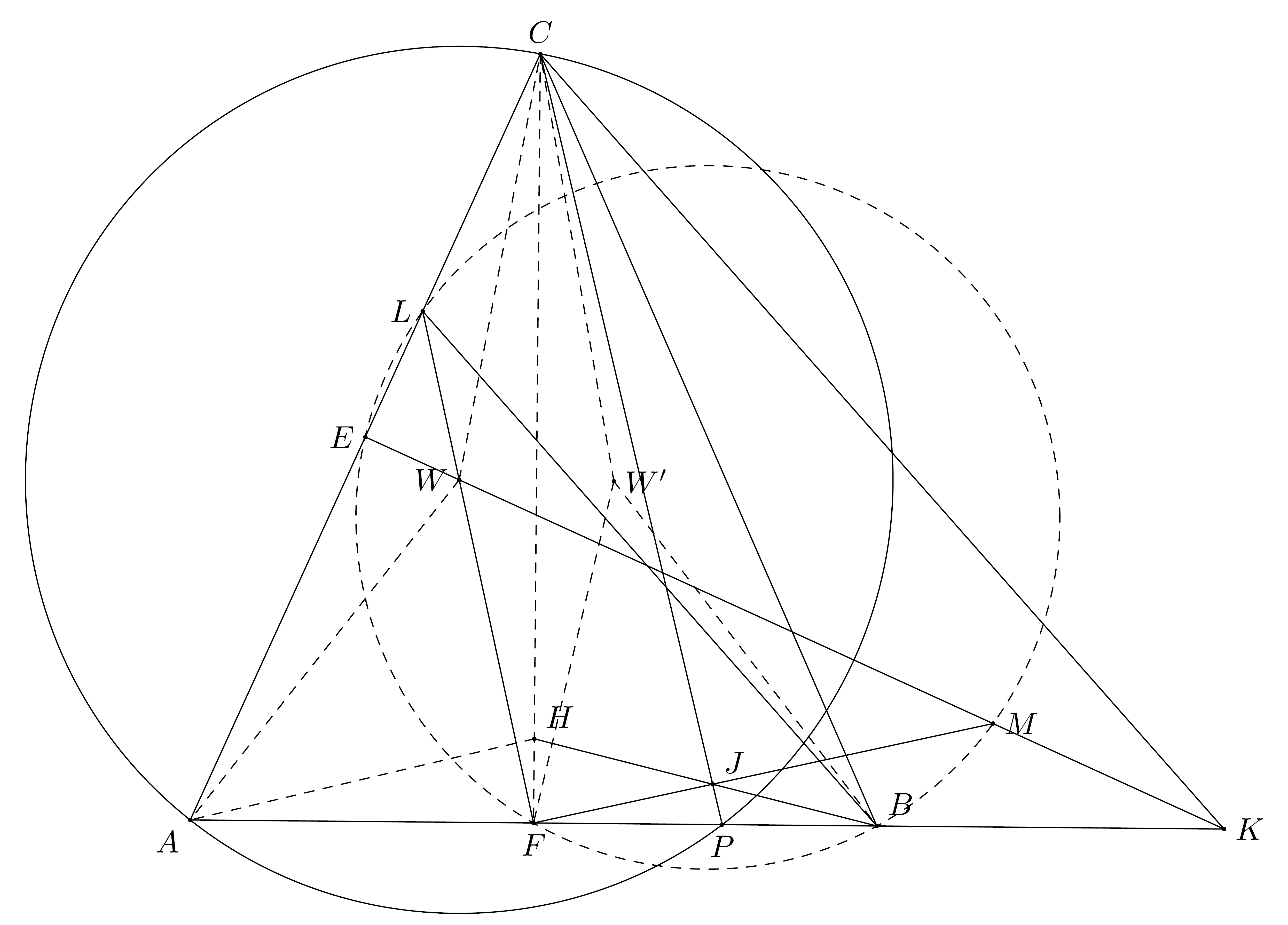
用等角共轭解决2014年韩国数学奥林匹克P2几何
https://gooodpig.pages.dev/year/05/30/用等角共轭解决2014年韩国数学奥林匹克P2几何/