对XMO 19th的两道几何题的解答
二试P2
证明. 因为\(E\),\(F\)关于\(\triangle ABC\)等角共轭,所以\(\angle BAF=\angle CAE\).由\((AEDF)\),\[180^\circ=\angle AEC+\angle AFB=180^\circ-\angle BAF-\angle ABC+180^\circ-\angle EAC-\angle ACE.\] \[\therefore \angle BAF+\angle ABC=\angle EAC+\angle ACE=\frac12(\angle BAF+\angle ABC+\angle EAC+\angle ACE)=90^\circ.\] \(\therefore AF\perp EH,AE\perp CE\)有\((AEHC),(AFHB)\), \[\angle EBH+\angle EHB=90^\circ+\angle EBH-\angle AHE=90^\circ+\angle EBH-\angle ACE=90^\circ.\] \(\therefore BE\perp EH\),同理\(CF\perp FH\).
\(\because AH\perp BC\therefore AB^2-AC^2=BH^2-HC^2.\)
设\(\angle EBH=\angle FCH=\theta\),\(BH=x\),\(CH=y\).由余弦定理\[\begin{cases}CE^2=x^2\cos^2\theta+(x+y)^2-2x(x+y)\cos^2\theta,\\BF^2=y^2\cos^2\theta+(x+y)^2-2y(x+y)\cos^2\theta.\end{cases}\] \(\therefore BF^2-CE^2=(x\cos\theta)^2-(y\cos\theta)^2=BE^2-CF^2.\) \[\begin{align*}DE^2-DF^2&=(AD^2-AE^2)-(AD^2-AF^2)\\&=(AB^2-BF^2)-(AC^2-CE^2)\\&=(AB^2-AC^2)-(BF^2-CE^2)\\&=(BH^2-HC^2)-(BE^2-CF^2)\\&=(BH^2-BE^2)-(CH^2-CF^2)\\&=HE^2-HF^2.\end{align*}\] \(\therefore HD\perp EF.\square\)
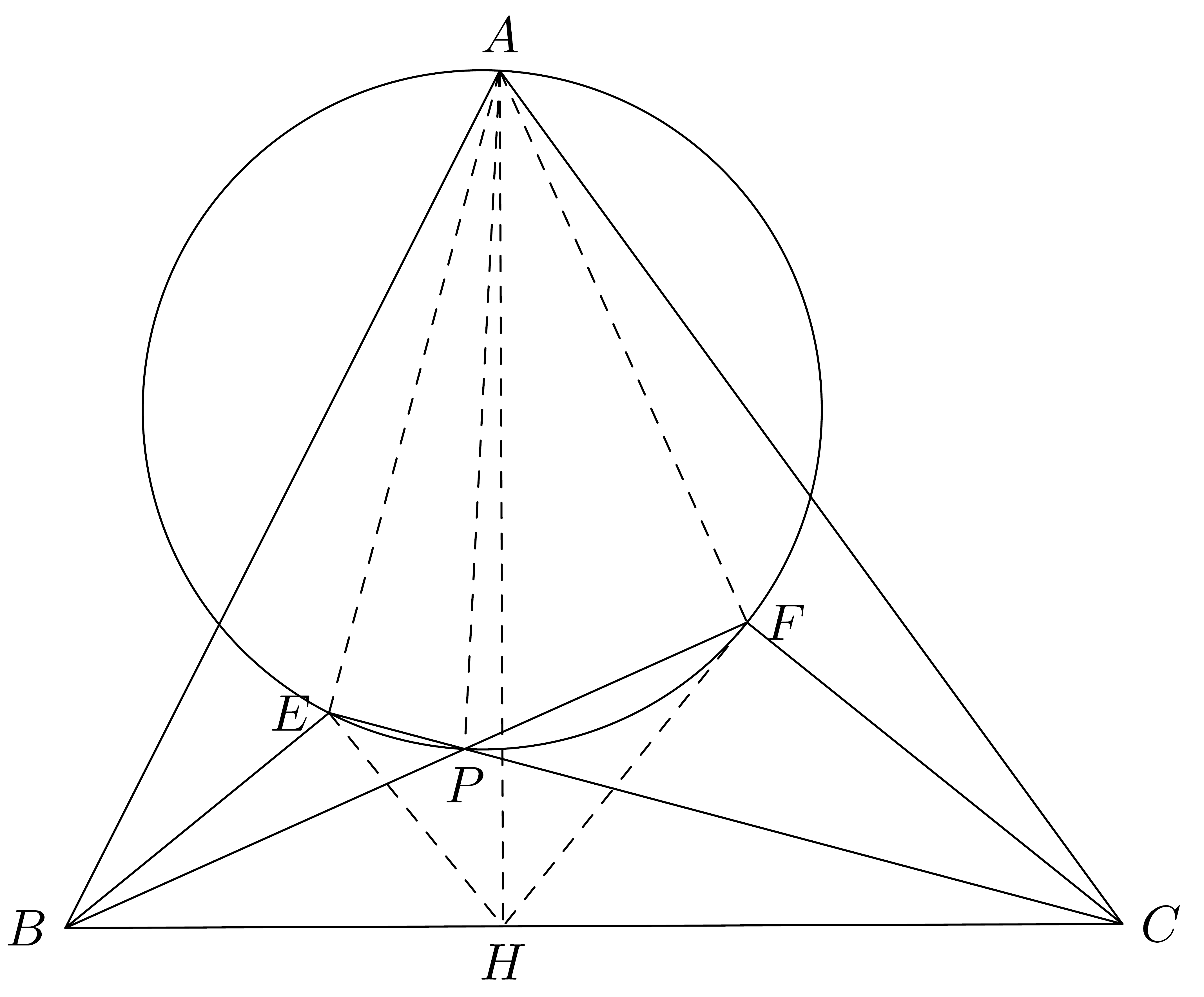
一试P9(纯几何)
乖猪玩原神去了,等会再写.