乖猪的几何缝合怪题集

这个题集主要是把乖猪平时做到的几何缝合起来,变成一个新题.

问题1

题目 如图,设\(\triangle ABC\)的内心是\(I\),外接圆\(O\).\(AI\)与\(\odot O\)再次交于\(A_1\),\(A_2\)是\(BC\)中点,\(A_3\)是\(\triangle AA_1A_2\)外心,\(A_4\)是\(IA_1\)中点,\(A_5\)是\(AI\)中点,过\(A_5\)且垂直于\(AI\)的直线交过\(A_1\)且垂直于\(A_3A_4\)的直线于\(A_6\),\(I\)在\(BC\)上的射影是\(A_7\),\(A_7\)关于\(A_2\)的射影是\(A_8\),过\(A_8\)作\(OA_6\)的平行线\(l_a\).类似定义\(l_b,l_c\).证明:\(l_a,l_b,l_c\)交于一点.

图

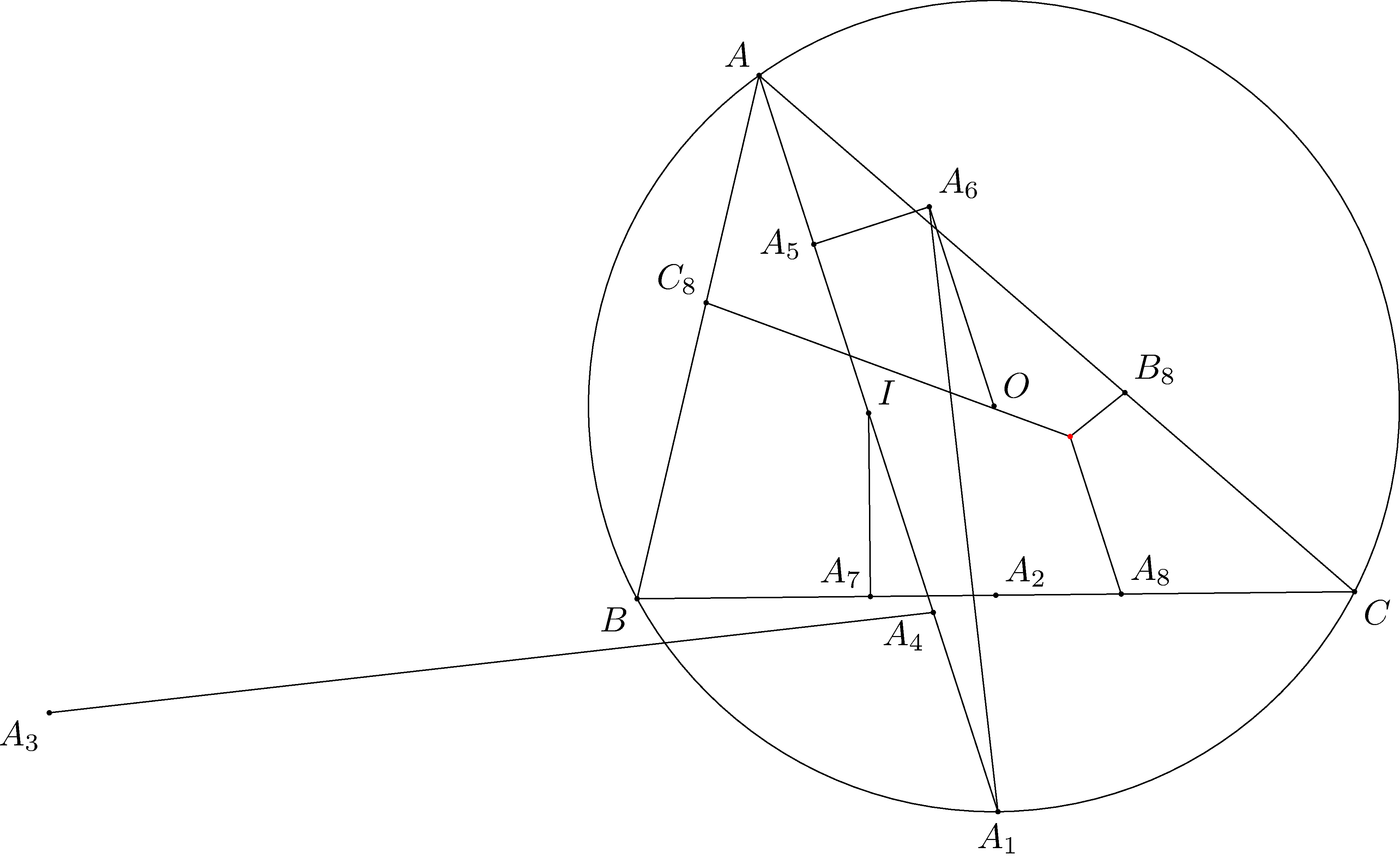
评注 把上一道题的结论和下一道题的条件拼在一起,你就得到了一道新题!

问题2

题目 如图,\(M,N,P,Q,R,S\)都是切点.过\(R,S\)作\(BC\)的垂线,交\(MN,PQ\)于\(G_1,G_2\).若\(G_1,G_2\)是\(\triangle ABC,BCD\)的重心,证明:\(AP,DM\)的交点在两圆的一条公切线上.

图

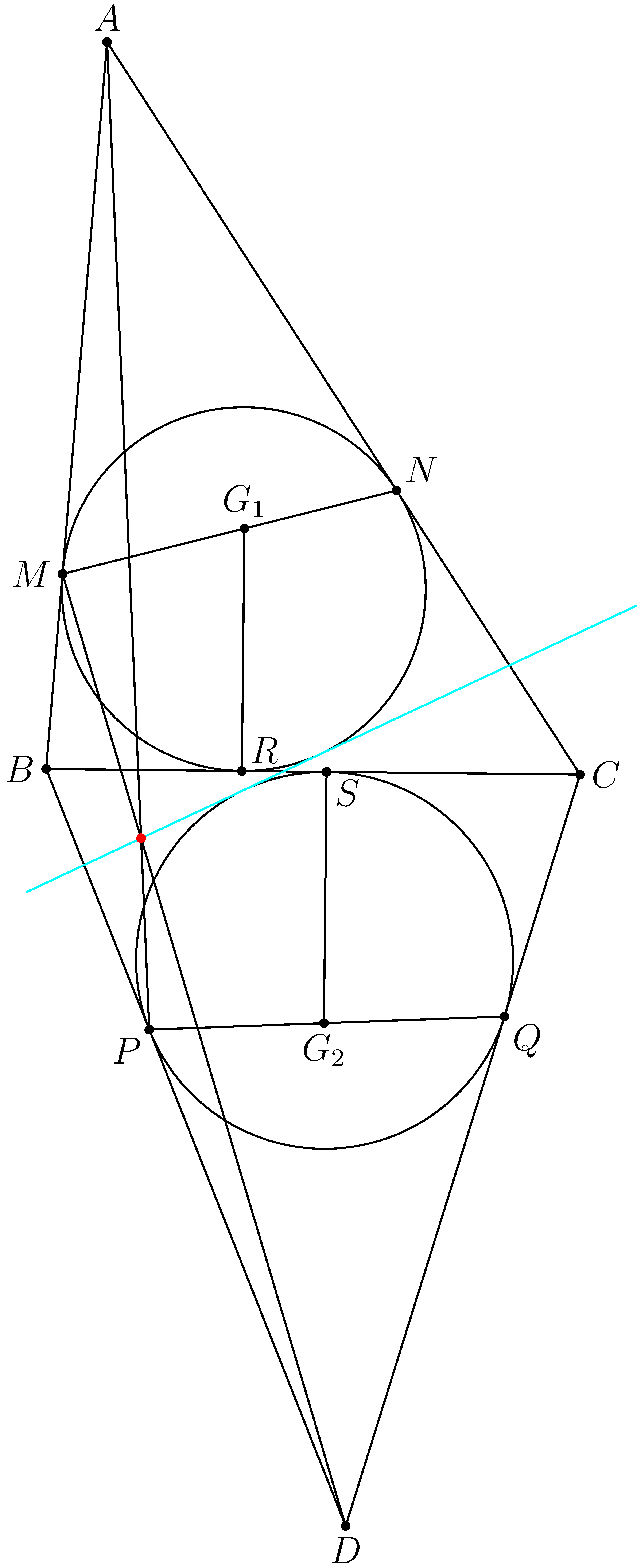
评注 把上一道题的中间过程和下一道题的条件拼在一起,你就得到了一道新题!

警告 由于乖猪的胡乱拼接,本题的条件和结论不是充要的.