【干货】高中「解三角形」问题杂集

叠甲

这个博客属于整活,致力于使用猎奇的辅助线或猎奇的恒等变形解决课内题.

警告 如果你有以下情况之一,请立刻离开:

1. 你的解三角形基础薄弱,本来就不会做;

2. 你对初中学的平面几何知识毫无了解;

3. 你不会配方法.

好消息 如果你有以下情况,这份文档或许对你有帮助:

1. 你在找乐子;

2. 你不喜欢高中数学里形式化、模板化的解三角形题目;

3. 你想学一些平面几何知识在学校装x.

第1题

题目 \(\triangle ABC\),\(D\)为\(BC\)上靠近\(B\)的三等分点,\(\angle DAB=2\angle DAC,AD=1\),求\(BC\)的取值范围.

为此,我们证明一个引理:

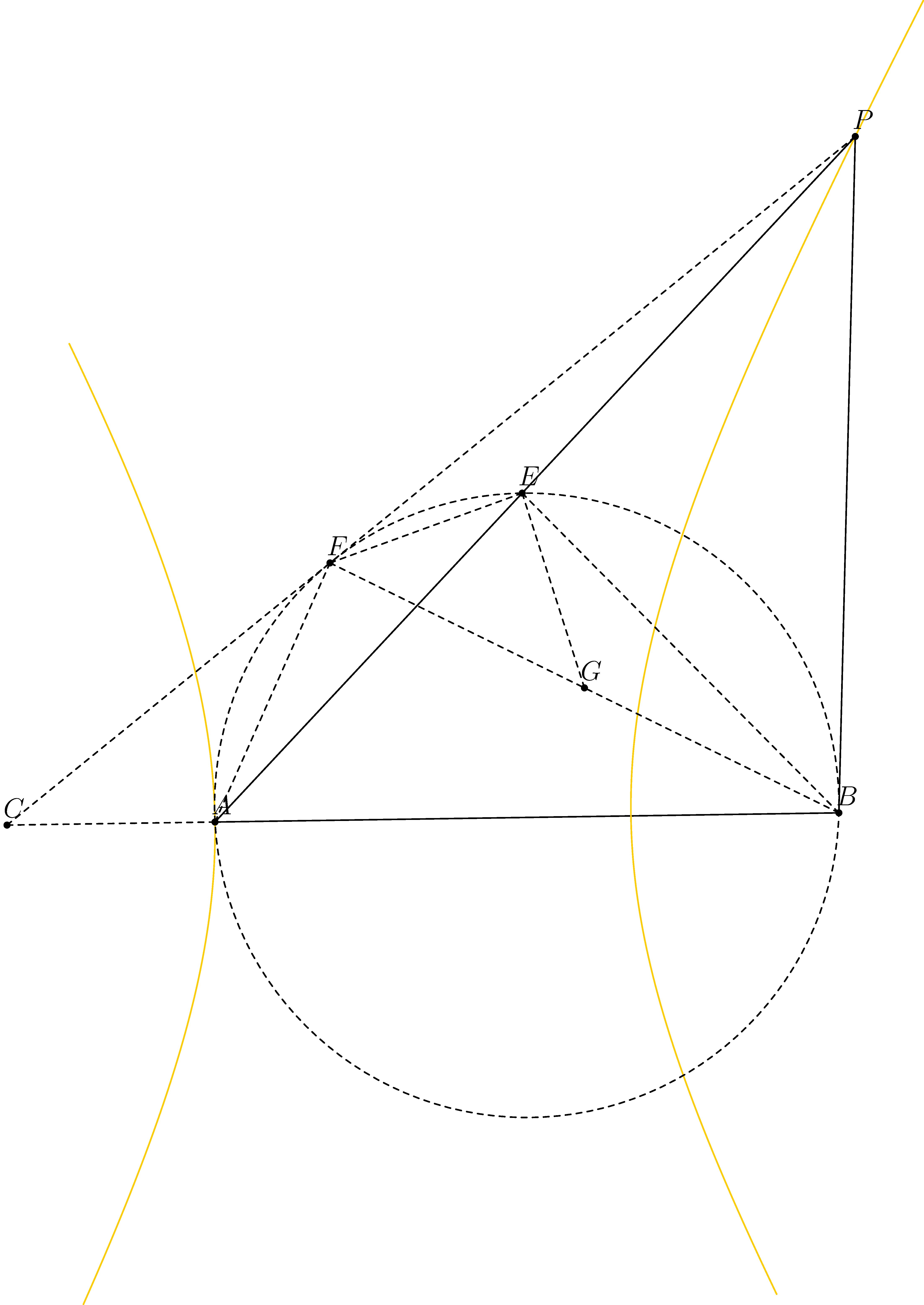
Lem. 如图,\(A,B\)是定点,\(P\)是动点满足\(\angle PAB=2\angle PBA\),则\(P\)的轨迹是双曲线的一支.

Prf1(利用双曲线的第一定义). 如图,\(BE\)是角平分线,\(\angle PBE=\angle EBA=\angle PAB\).由弦切角定理,\(\odot ABE\)与\(BP\)相切.作另一条切线,切点是\(F\),与\(AB\)交于\(C\).设\(G\)是\(BF\)中点.熟知四边形\(ABEF\)是调和四边形,\(\triangle EBG\sim\triangle EAF\).但\(AE=BE\Rightarrow AF=BG=\frac12BF\),而\(\triangle CAF\sim\triangle CFB\),计算比例可知\(AC=\frac13 AB,CF=\frac23 AB\).于是\(C\)也是定点,但\(PC-PB=PC-PF=CF=\frac23AB\),即\(P\)的轨迹是双曲线的一支.\(\square\)

Remark.想到这个做法时,乖猪还不知道圆锥曲线的第二定义.

Prf2(利用双曲线的第二定义).

不想敲了发个网图(

prf2

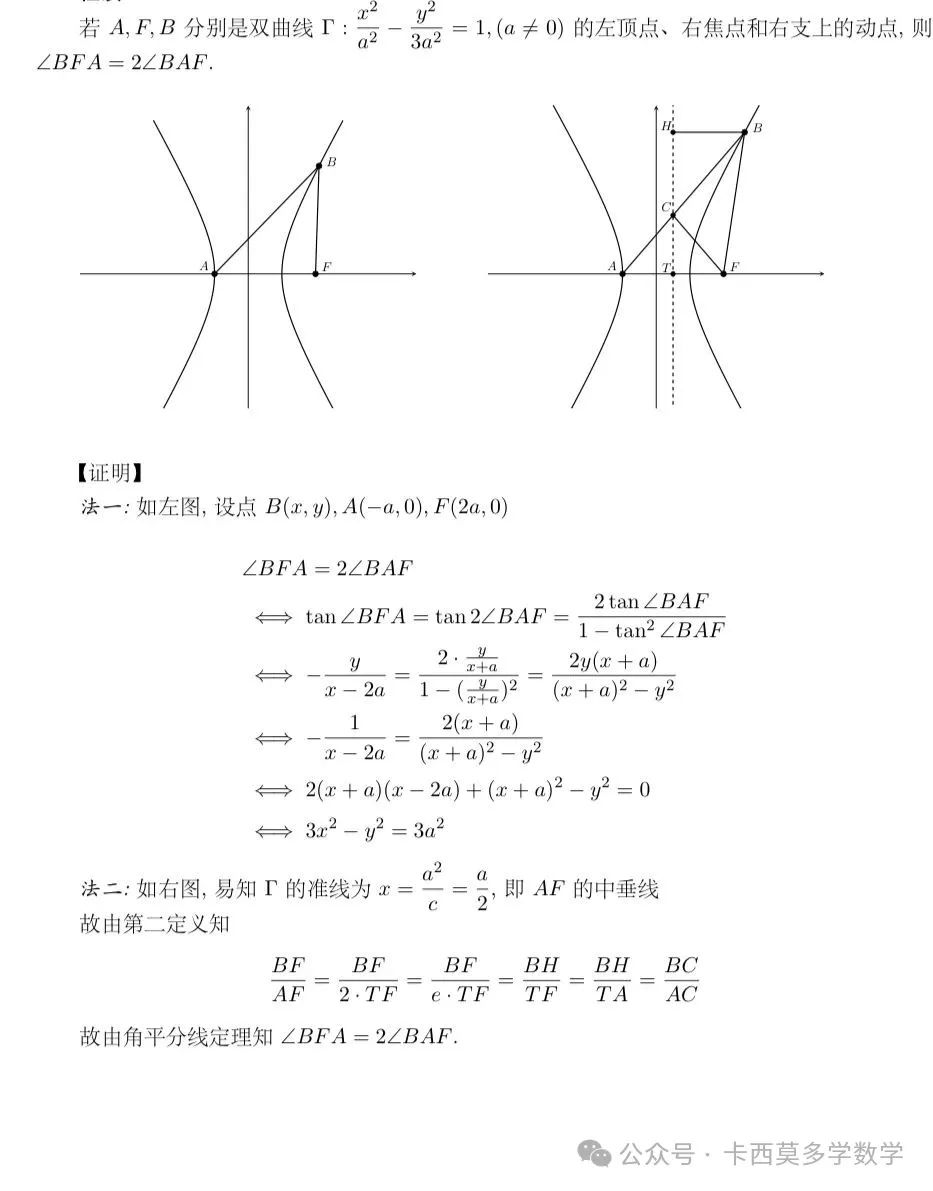
回到原题 显然.

第二题

题目 \(\triangle ABC\),\(2\sin^2A+\sin^2B=2\sin^2C\).求\(\sum_{\mathrm{cyc}}\cot A\)的最小值.